「対偶の論理は聞いたこと有るけれど、実際の使い方なんてわからない」という方、『対偶の論理』は、実生活で使える論理だということを知って下さい。『対偶の論理』を使うと、日常の会話で生まれる些細な違和感を、論理的に解決出来るかもしれません。
この記事では、『対偶の論理』の活用方法を解説していきます。

『それっぽい話』に対する些細な違和感
もし「人気があるお店は、明るい店内である」という推察が有るとして、この命題は正しいでしょうか。店内が明るいお店が人気があるというのは、それっぽい推察ですが・・・ 続きは記事後半で説明しています。
対偶の論理を使って物事の証明を行う
命題「AならばB」のAとBを入れ替えて両方否定形にした「BでないならAでない」という文章を対偶と言います。対偶と元の命題の真偽は一致します。要するに命題が正しい場合、その対偶は必ず正しく、対偶が正しければ元の命題も必ず正しいということです。
この法則を使って物事を論理的に解決することを論理の相関図にして解説します。
対偶と元の命題の関係
対偶とは、元の命題に対する『逆の論理』をさらに『裏の論理』にしたものです。逆と裏は真偽がひっくり返りますので、逆の裏は2度ひっくり返り元に戻る事になります。
相関図で見る『対偶の論理』
対偶の論理を上手に活用するには、この図の4つの象限に対しての真と偽の関係を理解することが大切です。図の中央に注目して下さい。それぞれ対偶の関係にある場合、真偽が一致しています。これによって破綻した論理などを見抜くことが出来るのです。
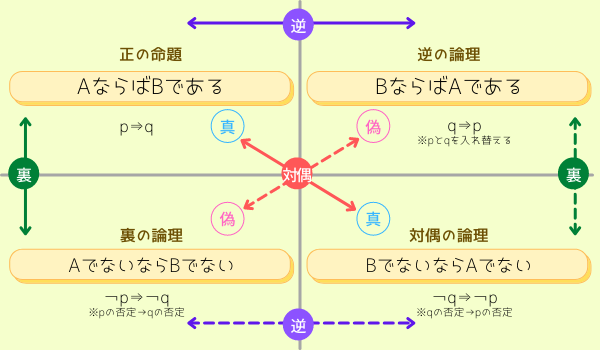

この図でわかるように、命題と対偶は対頂角にあります。ポイントは、命題の真偽と対偶の真偽は必ず一致するということです。
対偶の論理は、命題の真偽を証明できる
命題「AならばB」の真偽を証明することが難しい場合に、その対偶の「BでないならAでない」の証明が比較的容易なことがあります。対偶の証明を行い、元の命題の証明が出来るのです。このことが、些細な違和感を論理的に証明するポイントになります。
対偶の論理、裏の論理、逆の論理については別の記事で詳しく解説しています。
合わせてこちらも、ご覧ください。
対偶の論理 活用方法
特別なことではなく、日常的にちょっとした計画を立てる時なんかにも『対偶の論理』は活用できます。もしかしたら、今までも無意識に使っているのかもしれませんが、上手に活用するなら、理解している方が良いかもしれません。
論理構築のチェックに『対偶の論理』を活用する
論理を構築や、計画を立てるときなどに、目的に沿った行動の計画が立てられているかを確認をしますよね。そんな時に、対偶の論理を使ってチェックしてみると、真だと思っていた計画(命題)に対して、対偶では偽になっていることで間違いに気づくことがあります。
他者の発言や主張の違和感を見抜く
『対偶の論理』を使うと他者の論理展開が破綻しているか、成立しているのかを見分けやすくなります。案外それっぽい論理だと、納得してしまいそうになる事があります。しかし、対偶にしてみると例外がたくさんあるので、論理破綻に気付けるのです。それっぽさに引っ張られないように対偶を使えるようにして下さい。

冒頭の話の続きです!
「人気があるお店は、店内が明るい」というのは対偶にしてみると、「店内が明るくないお店は、人気がない」となってしまいます。店内が薄暗いお店でも人気のあるお店は世の中に沢山ありますので、このそれっぽい推察は偽です。
対偶の論理 注意点
論理構築に有効な『対偶の論理』ですが、使い方を間違えるとうまくいかないこともあります。ここでは注意点を2つ紹介します。
使用する品詞に注意する
命題「AならばB」を対偶にする時に注意することは、AとBの品詞です。AとBが動詞や形容詞などで文章ができている場合、違う意味になることがあります。そもそも、『対偶の論理』は名詞をくくった集合の論理です。ですから、AとBを名詞にしなければ集合として成り立たなくなってしまうのです。

注意点その①
命題「AならばB」のAとBは名詞化してから対偶にすることがポイントです!
具体的には以下の例文を確認して下さい。
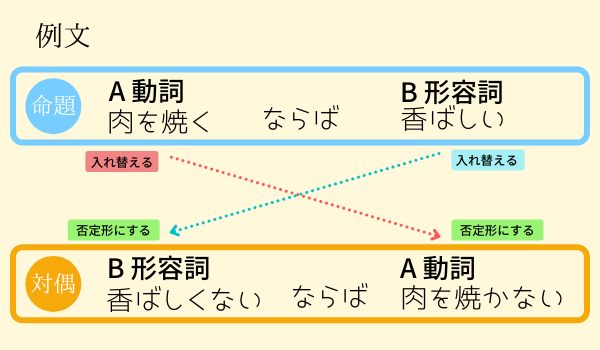

上の例文は、日本語としてもおかしいですが、そこは無視したとしても対偶にした時に全く意味が違うようになってしまいます。
そんな時は、下の例文のように、名詞に言い換えてから対偶にする必要があります。
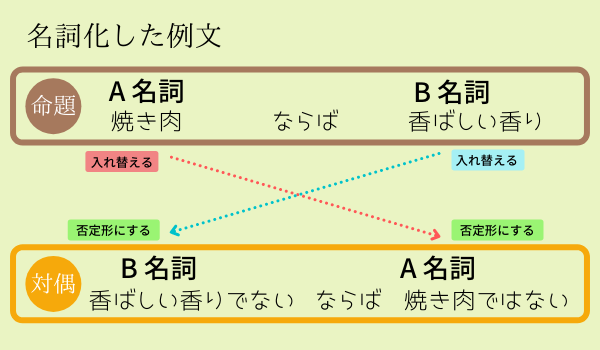
否定する言葉のチョイスに注意
命題を対偶にする時、否定形の言葉のチョイスを間違うと意味が変わってしまうこともあります。例えば、「美味しい料理」を否定するために対義語の「不味い料理」という言葉をもってくると、極端な言い切りになってしまいます。極端に言い切ると「美味しい料理」以外は全て「不味い料理」のようになってしまうので極端な言い切りは注意して下さい。

注意点その②
否定形にする時は極端な言い切りの形にすると、命題にも対偶にも含まれない物が出てきて、論理が破綻してしまうことがあります。
ロジカルシンキングについて参考記事紹介
ロジカルシンキングについて、帰納法や演繹法を別記事で紹介しています。気になった方は、こちらからそれぞれの記事をご覧になれます。
最後までご覧いただき、ありがとうございます。






