【ロジカルシンキング】【論理的思考】『対偶の論理』について基本的な定義

という方に、「対偶の論理」について解説します！
まず、『対偶』という言葉の定義は、「対になっているもの」「2つで一揃い」「類」「仲間」という意味を持ちます。論理学で『対偶』とは、「命題に対する対の関係で真偽が一致するもの」と定義。この記事では、論理学上『対偶』の定義が何を意味し、どうやって使うことが出来るのか紹介します。

対偶の論理は命題と真偽が一致する

『対偶の論理』は、「高校時代に数学で習った気がするけど内容は覚えていない」という方、もう一度『対偶の論理』を理解してみてはいかがでしょうか。『対偶の論理』を理解していれば、課題の解決や、物事の真偽を見極めることに役立ちます。

『対偶の論理』は、AとBを入れ替えて否定形にする

命題『AならばBである』の対偶の論理とは、AとBを入れ替え、それぞれを否定にした形『BでないのならAではない』となります。

この命題が真となるとき、対偶も真となり、命題が偽となるときは対偶も偽となります。おそらく高校の数学で「p⇒q」とその対偶「￢q⇒￢p」という形で習っていたのではないでしょうか。

【図解】対偶の論理の例題

命題を『オムレツは卵料理である』とします。
この命題の対偶は、『卵料理でないのであればオムレツではない』となります。
上の図のようにAとBを入れ替え、それぞれを否定形にします。もちろんオムレツは卵料理なので命題は真で、その対偶も真となります。

この命題が真となる理由は、主部となるAが、述部のBの領域に属しているからなのです。下の図の様にAよりBが大きな領域で、且つAがBの中に属している場合、命題は真となります。

言葉の定義解説

用語	解説
命題	「Yes」または「No」で答えられる文章のこと
真	命題の答えが「Yes」となる場合 その文章が成り立っている状態を真という
偽	命題の答えが「No」となる場合 その文章が成り立たない状態を偽という
逆の論理	命題の主部Aと述部Bを入れ替えたもの
裏の論理	正の命題の主部Aと述部Bをそれぞれ否定形にしたもの

逆・裏・対偶の相関関係

前項でも解説しましたが、『命題』に対して、AとBを入れ替えたものが『逆の論理』で、『命題』のA、Bともに否定したものが『裏の論理』となり、AとBを入れ替えそれぞれ否定したものが『対偶の論理』です。これらの関係を図にしましたので、こちらで整理してみて下さい。

『対偶の論理』は逆の裏

下の相関図でご覧いただければわかるのですが、対偶は『裏の論理』から見れば逆になり、『逆の論理』から見れば裏になります・・・。
言葉にすると、ややこしいので、ポイントをひとつ確認して下さい。「それぞれ対偶の関係にある場合、その真偽は一致する」ということです。

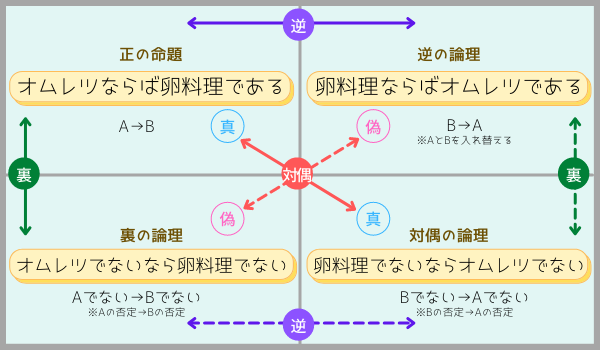
※逆の論理の「卵料理ならばオムレツである」は、オムレツ以外の卵料理が無数に存在するため偽となります。また、裏の論理の「オムレツでないなら卵料理でない」も同様にオムレツでない卵料理はたくさんあるので偽となります。

『逆の論理』・『裏の論理』

今回は対偶の論理についての解説ですが、『逆の論理』や『裏の論理』も同様に理解が必要となります。『逆の論理』・『裏の論理』については別の記事で解説していますので、こちらもご覧ください。

対偶の論理の活用

対偶の論理を上手に使えるようになると、間違った論理展開をしている場合、それを見抜けるようになります。

例えば、自分が組み立てた論理を検証する場合は、その論旨の対偶を使って真偽が一致しない場合、論理展開に無理があるとわかります。

対偶を使った具体的な活用方法は、別の記事で紹介していますので、よかったらこちらからご覧ください。

ここまでご覧いただき、ありがとうございます。